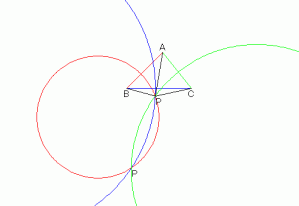
点 P を作図する手順。
D1D2 を直径にもつ円(アポロニウスの円)を描く。
ただし, α=β のときは,AB の垂直二等分線を描く。
(2) BC を β:γ に内分する点 E1 と外分する点 E2 を求め,
E1E2 を直径にもつ円(アポロニウスの円)を描く。
ただし, β=γ のときは,BC の垂直二等分線を描く。
(3) (1)と(2)の交点が P である。
|αBC−βCA|≦γAB≦αBC+βCA
| 問題 |
3点 A,B,C と,それらからの距離の比 AP:BP:CP=α:β:γ が与えられたとき, 点 P を作図する手順。 |
|---|---|
| 解答 |
(1) AB を α:β に内分する点 D1 と外分する点 D2 を求め, D1D2 を直径にもつ円(アポロニウスの円)を描く。 ただし, α=β のときは,AB の垂直二等分線を描く。 (2) BC を β:γ に内分する点 E1 と外分する点 E2 を求め, E1E2 を直径にもつ円(アポロニウスの円)を描く。 ただし, β=γ のときは,BC の垂直二等分線を描く。 (3) (1)と(2)の交点が P である。  |
| 条件 |
P が存在する条件 |αBC−βCA|≦γAB≦αBC+βCA |