数学T　三角比

三角比を学ぶ意義

天下り的に定義と公式を教えるのではなく， 三角比の概念が考え出される過程を説明する．
また，わかりやすい特殊な場合から始めて，徐々に一般的な場合に拡張していく，という 数学の手法を理解させる．
もちろん，この説明も一方的に話すのではなく，随時生徒の発言を求める．

相似（形が同じ）と合同（形も大きさも同じ）の概念を思い出す．

A判の紙とB判の紙と名刺を配る． それらは相似か？
それぞれを半分にした長方形と，元の長方形は相似か？
答を確かめるにはどうしたらよいか？
それぞれを対角線で切った三角形を重ねて比べ，3つの角が一致すれば相似で， 元の長方形も相似である． 三角形の角の和は180゜であるから，2つの書くが一致すればよく， 今の問題では，1つの角が直角であるから，最小の角を重ねて調べるだけでわかる．
四角形の場合，4つの角がそれぞれ等しくても相似とは限らないが， 三角形の場合，2つの角がそれぞれ等しければ相似である．

二つの三角形△ABC と△A'B'C' が相似であること，および合同であることの条件を思い出す．

二角相似定理
A=A',B=B' ならば相似である．
A,B が決まれば C と a:b:c が決まる．
二角挟辺合同定理
A=A',B=B',c=c' ならば合同である．
A,B と c が決まれば C と a,b が決まる．
二辺挟角合同定理
A=A',b=b',c=c' ならば合同である．
a,b と C が決まれば c と A,B が決まる．
三辺合同定理
a=a',b=b',c=c' ならば合同である．
a,b,c が決まれば A,B,C が決まる．

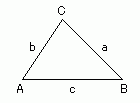
このことから，自ずと次の問題が思い浮かぶ．

問題
(1) 角 A,B が与えられたとき，残りの角 C の求め方を知りたい．
(2) 角 A,B が与えられたとき，三辺の比 a:b:c の表し方を知りたい．
(3) 角 A,B と辺 c が与えられたとき，他の辺 a,b の求め方を知りたい．
(4) 辺 a,b と角 C が与えられたとき，残りの辺 c の求め方を知りたい．
(5) 辺 a,b と角 C が与えられたとき，他の角 A,B の求め方を知りたい．
(6) 辺 a,b,c が与えられたとき，角 A,B,C の求め方を知りたい．
答え
(1) A,B から C を求める式がある．
　　　C=180゜-A-B
(2) (1)より，A,B,C が与えられたとしてよい．
　　これについて後で考える．………@
(3) (2)の式があれば，c から a,b を求められる．
(4) これについても後で考える． ……A
(5) (4)と(6)がわかればよい．
(6) これについても後で考える． ……B

@,A,Bについて考える．

初めからすべての三角形を対象に考えるのではなく， わりやすい三角形から考えていく．
すなわち，直角三角形→鋭角三角形→鈍角三角形 の順に考えていく．

直角三角形の場合

角 C=90゜とする．
角 A を決めると角 B と3辺の比 a:b:c が決まる． すなわち，a/c, b/c, a/b が決まる．
この値をそれぞれ A の正弦(sine)，余弦(cosine)，正接(tangent)といい， sin A，cos A，tan A で表す．
　　sin A = a/c = (A の)対辺/斜辺
　　cos A = b/c = (A の)隣辺/斜辺
　　tan A = a/b = (A の)対辺/(A の)隣辺
である．
角 B については，
　　sin B = (B の)対辺/斜辺 = b/c
　　cos B = (B の)隣辺/斜辺 = a/c
　　tan B = (B の)対辺/(B の)隣辺 = b/a
となる． これを見ると，
　　cos A = sin B
　　cos B = sin A
となっている．
A と B のように和が90゜になる2つの角を互いに余角(complementary angle)という．
余弦(cosine)は余角(co-angle)の正弦(sine)（cos A = sin(90゜-A)）という意味である．
同じ考え方で，余角の正接を余接(cotangent)（cot A = tan(90゜-A)）という．
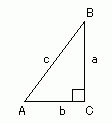
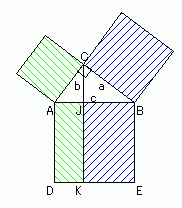
@(C=90゜の場合)について
　　a : b : c = c sin A : c sin B : c = sin A : sin B : 1
sin 90゜ = 1 　（したがって cos 0゜= 1）と定める．
　　a : b : c = sin A : sin B : sin C

A(C=90゜の場合)について
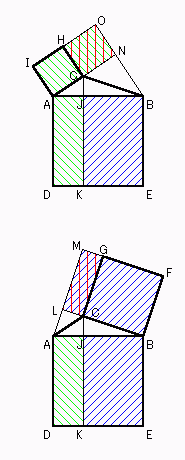
　□ADKJ = AD・AJ = c・b cos A = b・c cos A = b2
　□BEKJ = BE・BJ = c・a cos B = a・c cos B = a2
ゆえに，
　　c2 = a2 + b2
　　a2 = c2 - b2
　　b2 = c2 - a2
このように，2辺から他の辺を求めることができる． しかし，c を求める式と a,b を求める式の形が異なる． これは，2辺だけを用いているからである． 間の角を用いると同じ形の式で表すことができるが， それは鋭角三角形の場合に含めて考えることにする．

B(C=90゜の場合)について
sin A または cos A の値がわかったら，角 A がわかったと考える．
　　sin A = a/c ,　　sin B = b/c ,　　C = 90゜

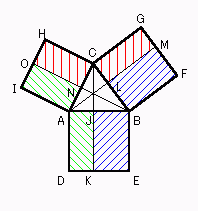
鋭角三角形の場合

@(鋭角三角形の場合)について
CA sin A = CJ = CB sin B より
　　a : b = sin A : sin B
同様に
　　b : c = sin B : sin C
これより，次の正弦定理が得られる．
　　a : b : c = sin A : sin B : sin C

A(鋭角三角形の場合)について
　　■ADKJ = AD・AJ = cb cos A = bc cos A = AI・AN = ■AION
同様に
　　■BEKJ = ■BFML = ca cos B
　　■CHON = ■CGML = ab cos C
したがって，たとえば
　　□ABED = □ACHI - ■CHON + □BCGF - ■CGML
これから，次の余弦定理が得られる．
　　c2 = a2 + b2 - 2ab cos C
　　a2 = b2 + c2 - 2bc cos A
　　b2 = c2 + a2 - 2ca cos B

直角三角形のA(C=90゜の場合)は余弦定理の特殊な場合である．
a を求める式は cos A = b/c という特殊な場合である．
b を求める式は cos B = a/c という特殊な場合である．
cos 90゜= 0 　（したがって sin 0゜= 0）と定める．
c を求める式は cos C = 0 という特殊な場合である．

B(鋭角三角形の場合)について
余弦定理の式を変形すればよい．
　　cos A = (b2 + c2 - a2)/(2bc)
　　cos B = (c2 + a2 - b2)/(2ca)
　　cos C = (a2 + b2 - c2)/(2ab)

鈍角三角形の場合

@(C が鈍角の場合)について
AB sin B = AL = AC sin (180゜-C) より
　　 b : c = sin B : sin(180゜-C)
鈍角 C について sin C = sin(180゜-C) と定める．
正弦定理が鈍角三角形でも成り立つ．
　　a : b : c = sin A : sin B : sin C

A(C が鈍角の場合)について
鋭角の場合と違って
　　■CHON = CH・CN = b a cos(180゜-C)
　　■CGML = CG・CL = a b cos(180゜-C)
　　□ABED = □ACHI + ■CHON + □BCGF + ■CGML
ゆえに
　　c2 = a2 + b2 + 2ab cos(180゜-C)
鈍角 C について cos C = - cos(180゜-C) と定める．
余弦定理が鈍角三角形でも成り立つ．
　　c2 = a2 + b2 - 2ab cos C
　　a2 = b2 + c2 - 2bc cos A
　　b2 = c2 + a2 - 2ca cos B

B(鈍角三角形の場合)について
やはり余弦定理の式を使えばよい．
　　cos A = (b2 + c2 - a2)/(2bc)
　　cos B = (c2 + a2 - b2)/(2ca)
　　cos C = (a2 + b2 - c2)/(2ab)